project 3

Face Morphing

Part 1: Defining Correspondences

I did not really want to manually label correspondences. After doing some research, I found dlib's shape_predictor_68_face_landmarks.dat which is a face landmark detector that labels 68 points on the face.

I was able to define correspondencess pretty easily since landmarks are consistent between faces. I noticed, however, that the landmarks did not cover the entire face. To get around this, I added 8 additional landmarks: the 4 corners of the image and the midpoints of the 4 edges.

I computed the midpoints between corresponding landmarks, and created the triangulation using scipy.spatial.Delauney (shoutout scipy as usual), which gave me the following:

Part 2: Computing the "Mid-way Face"

I represented each triangle composed of points \({(x_1, y_1), (x_2, y_2), (x_3, y_3)}\) as a 3 x 3 matrix: \[ \begin{bmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{bmatrix} \] the goal was to find a transformation matrix \(T\) such that: \[t_d = T t_s \] \[ \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} = T\begin{bmatrix} x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\ 1 & 1 & 1 \end{bmatrix} \] so I let \[ T = \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix}x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\1 & 1 & 1\end{bmatrix}^{-1}\] which yielded \[t_d = T t_s\] \[ \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} = \left( \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix}x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\ 1 & 1 & 1\end{bmatrix}^{-1} \right) \begin{bmatrix} x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\ 1 & 1 & 1 \end{bmatrix} \] \[ \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} \left( \begin{bmatrix}x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\ 1 & 1 & 1\end{bmatrix}^{-1} \begin{bmatrix} x_{s,1} & x_{s,2} & x_{s,3} \\ y_{s,1} & y_{s,2} & y_{s,3} \\ 1 & 1 & 1 \end{bmatrix} \right) \] \[ \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} I \] \[ \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} x_{d,1} & x_{d,2} & x_{d,3} \\ y_{d,1} & y_{d,2} & y_{d,3} \\ 1 & 1 & 1 \end{bmatrix} \] \[ t_d = t_d \] as desired.

This gave me an efficient way to get the affine transformation between corresponding triangles. By getting the inverse transformation for each triangle, I was able to compute the pixel in the source image correspoinding to each pixel in the destination image. To get the color for each pixel, I interpolated from the source image by using scipy.interpolate.RectBivariateSpline.

Here was the result I got from warping both images to the midpoint landmarks and performing a simple linear interpolation:

Part 3: The Morph Sequence

Part 4: The "Mean face" of a population

As my population, I used two sets of manually aligned frontal images from the FEI Face Database.

Part 5: Caricatures: Extrapolating from the mean

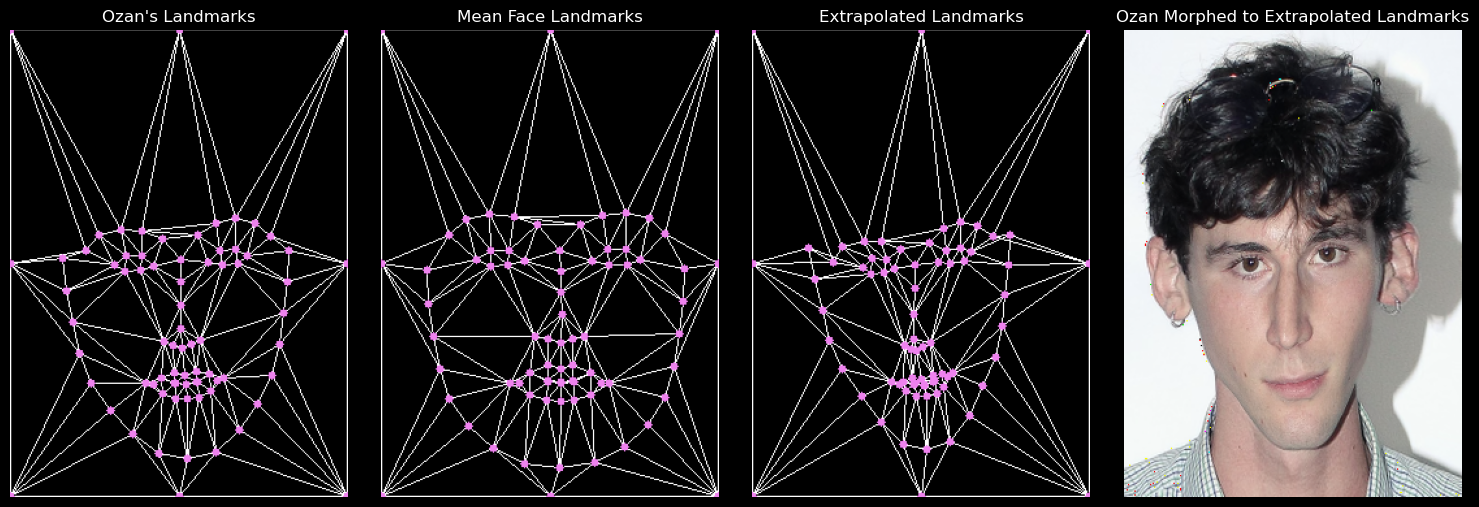
Using the mean landmarks of the FEI Dataset, I extrapolated a new set of landmarks: 1.8 * (My Landmarks) - 0.8 * (Mean Landmarks).

Here is the result of warping my face to these extrapolated landmarks:

Part 6: Bells and Whistles

I am Turkish. But could I look more Turkish? I wanted to see what it would look like if I morphed myself to the average Turkish man and woman.

I noticed my jaw tends to get distorted when I morph my face, so I tried it again, this time morphing the average faces to me.