project 6

Neural Radiance Field!


Part 1: Fit a Neural Field to a 2D Image

Implementation

For my initial implementation, I used what was recommended in the project description:

Results

Using the above parameters, I was able to fit a neural field to the image.

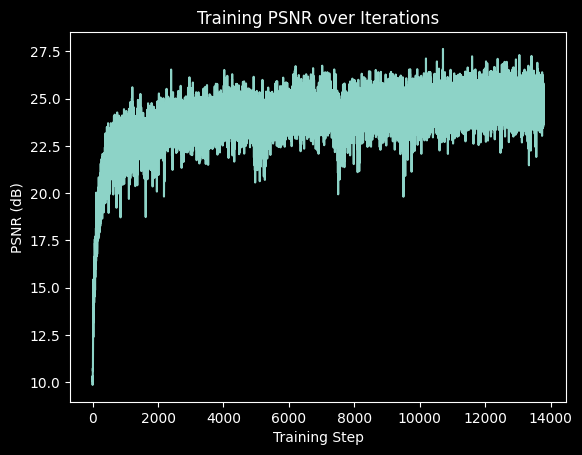
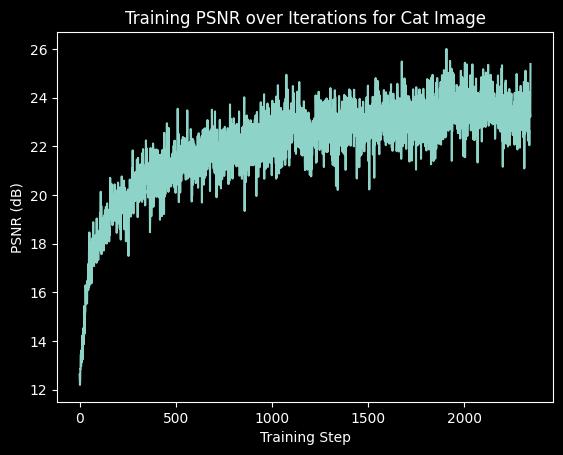
I fit the neural field to an image of my cat.

Hyperparameter Tuning

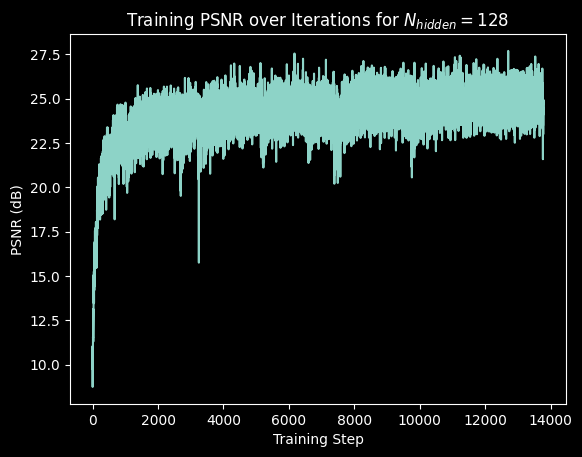
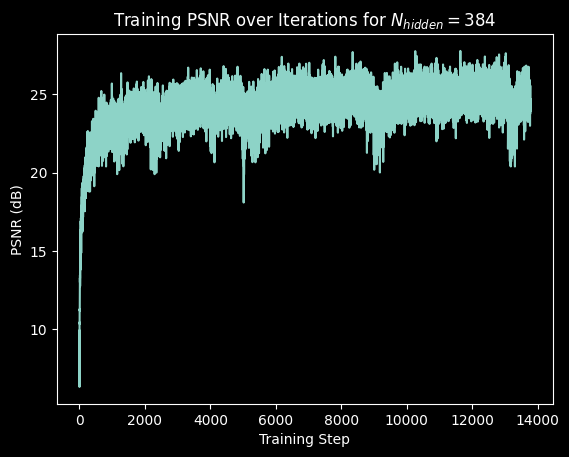
The hyperparameters I varied were the number of frequency bands and the hidden dimension size.

Varying the number of frequency bands generally led to worse results. The result of using 15 frequency bands was pretty interesting to me.

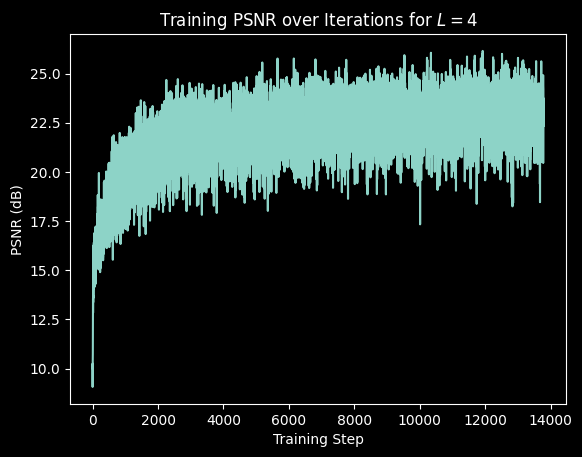
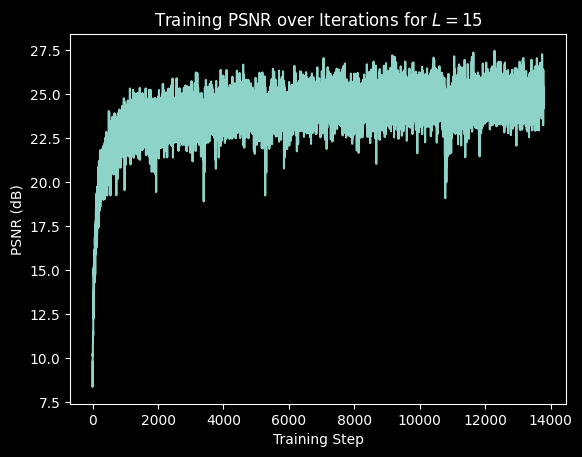
Altering the hidden dimension size did not have much of an effect on the results.

Part 2: Fit a Neural Radiance Field from Multi-view Images

2.1 Create Rays from Cameras

I implemented transform, pixel_to_camera, and pixel_to_ray using tensor operations. I used einops when I got sick of tensor wrangling.


2.2 Sampling Rays

I implemented sample_rays by first computing how many rays to sample from each image. I sampled this amount of pixel coordinates from each image, computed \(r_d, r_o\) using the appropriate camera parameters, and returned these rays alongside the ground truth pixel values. When the RaysDataset is initialized, it precomputes pixel coordinates and the corresponding rays for image 1 in order to support the visualization code.


2.3 Putting the Dataloading All Together


2.4 Implementing the NeRF

I initially implemented the NeRF as recommended in the project description. I wasn't sure if I had implemented it correctly, so I re-implemented it using nn.ModuleList to make it easier to adjust hyperparameters. My final parameters were:

  • 10-layer MLP + 1 density layer + 3-layer color MLP
  • 384 hidden dimensions
  • 10-band positional encoding


    • 2.5 Volume Rendering

    I compute \(a_i = \exp(-\sigma_i \delta_i) \) for all \(i\). This lets me find each \(T_i\) using torch.cumprod. I weight each color \(c_i\) by \(w_i = T_i a_i\) and compute \(\hat{C} = \sum_i w_i c_i\) to get the final color.


    2.6 Results

    128 samples per ray, 10000 rays per step, 10000 gradient steps (~3H on A1000 GPU).

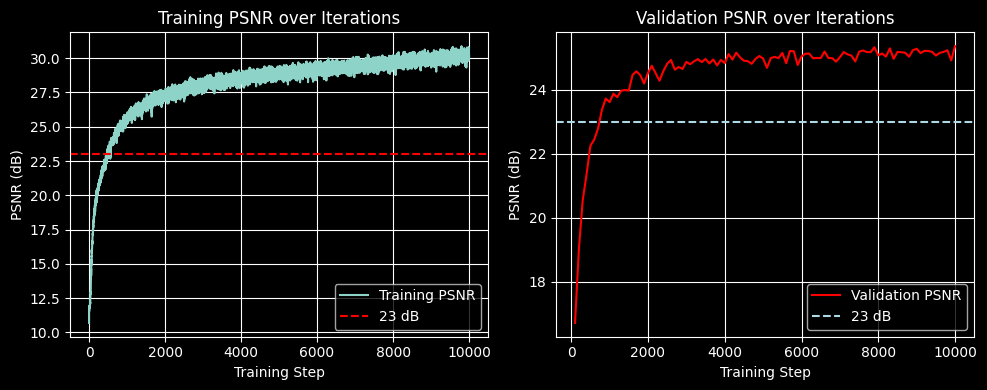
    (in a way, I made it to 30+ PSNR!)

    Bells and Whistles: New Background Color

    When rendering the pixel, I compute weights for the background with \( w_i = T_i(1 - a_i) \) and compute the final color as \( \hat{C}(r) = \sum_i T_i a_i c_i + T_i( 1- a_i) c_{\text{bg}} \).